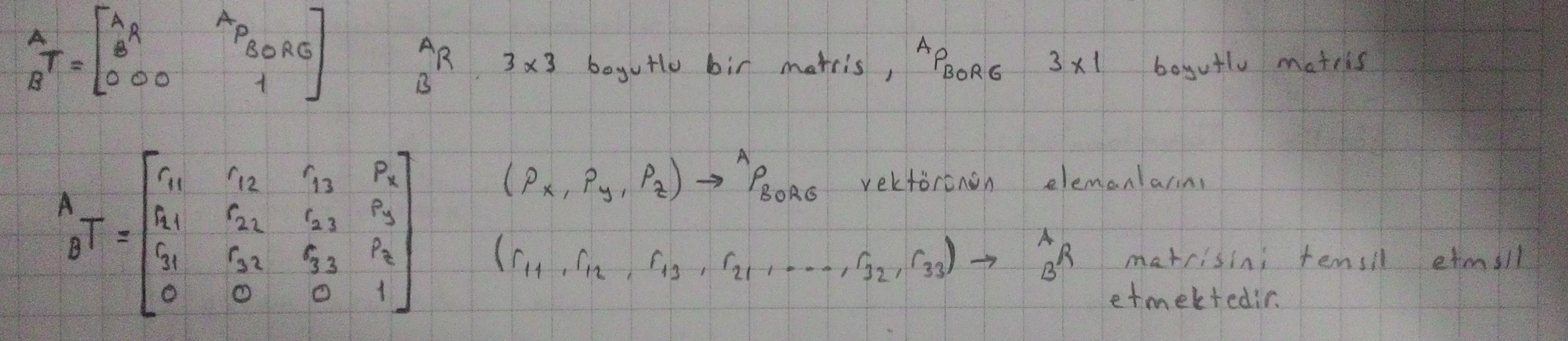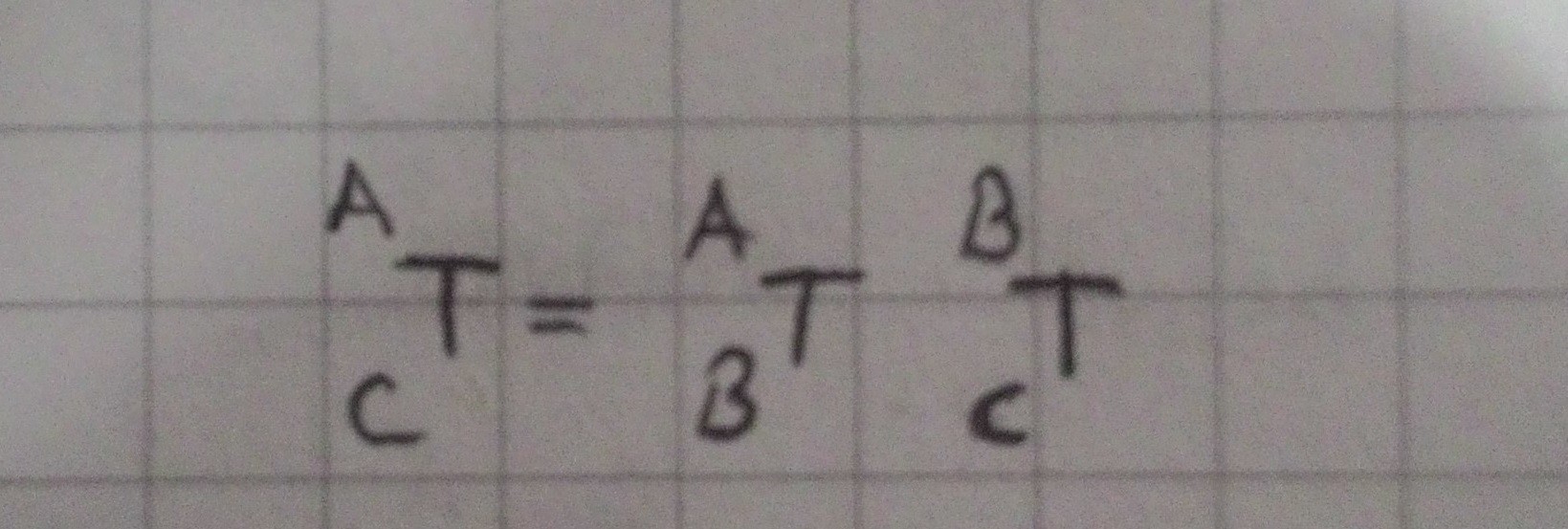Robot Kontrolüne Giriş
Endüstriyel Tarzı Bir Robotun Kontrolü
Robotlar ilk üç eklemin tipine göre bir takım harf sırası ile adlandırılır. Robot tiplerinde de görebileceğiniz gibi R ve P harfleri kullanılmıştır. Bu harflerden R ( Revolute ) dönel ve P ( Prismatic ) prizmatik bağlantı şeklini nitelendirmektedir. Şimdi kontrol için yazacağımız algoritmanın içerdiği bazı isimleri açıklayalım. "T" harfi ile gösterdiğimiz ( resimdede görebileceğiniz gibi ) dönme matrisi ve konum vektörünün bulunduğu 4x4 boyutunda bir matrisi ifade etmektedir. Dönme matrisi, bir A noktasının başka bir B noktasına göre iki noktada da yerleştirilmiş x,y,z koordinatlarının bir birine göre dönmesi tanımlanmaktadır. Konum matrisi, bir A noktasının başka bir B noktası ile arasındaki konum bilgilerini içermektedir.
Şimdi, tanımladığımız T dönüşüm matrisinin birden fazla birbirinden farklı koordinatların çarpımı olarak adlandırdığımız ardışık dönüşümü açıklayacağız. Üç ayrı {A}, {B} ve {C} koordinat sistemi var olsun. {C} koordinat sistemine göre tanımlanan bir P noktasını ardışık döşümü aşağıdaki gibi tanımlıyoruz.
Matrislerin çarpımı ile oluşan bu denklemler sayesinde artık, girdiğimiz açılar ile bir robotun uç noktasının konumlarını öğrenebileceğiz. Şimdi bu dönüşüm matrislerinin bir robot kontorlü için genellikle en çok kullanılan bir yöntemi göreceksiniz. Bu yöntemin adı Denavit-Hartenberg yöntemidir.
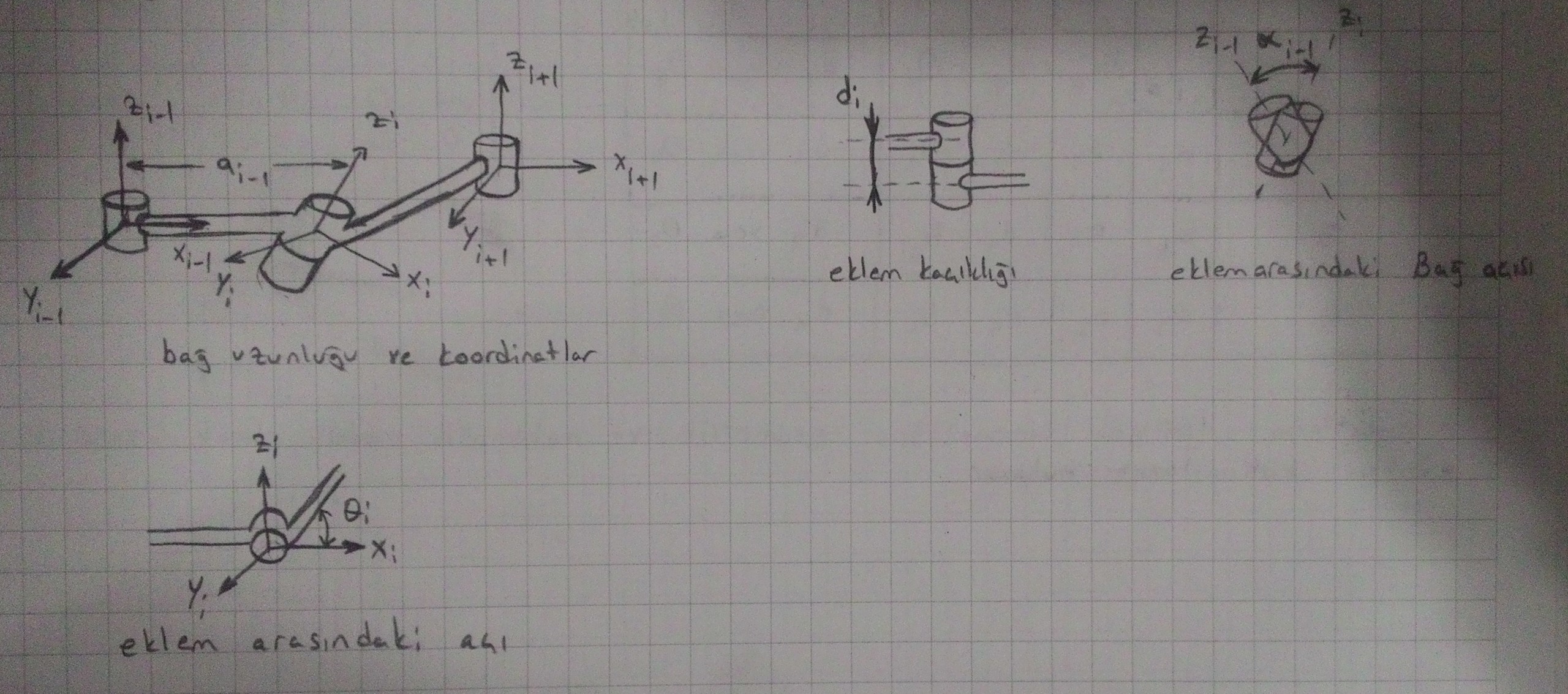
Yukarıdaki Şekilde gördüğünüz şekil ve ifadeler kullanacağımız yöntem için bilinmesi gereken tanımlama ifadeleridir. Bu ifadeler,
- a = iki eksen arasındaki bağ uzunluğu ( link Lenght )
- alfa = ( i-1 ) ile i ekseni arasındaki bağ açısı ( link twist )
- d = üst üste çakışan bağlar arasındaki eklem kaçıklığı ( joint offset )
- teta = iki bağ arasındaki oluşan eklem açısı ( joint angle )
Şeklinde tanımlanmıştır. Şimdi bütün yapılan tanımların bir DH tablosunda nasıl gösterileceğine bakalım.
Artık tabloyu doğru oluşturarak, ardışık dönüşüm matrislerinin yazılması ile birlikte bir robotun kontrolünü gerçekleştirmiş olacağız. Şimdi RRR tipinde dönel eklem yapısına sahip bir robot DH tablosu örneğine bakalım.
Yukarıdaki şekilde bulunan T dönüşüm matrisini yukarıdaki tabloda bulunan tanımları yerine koyarak dönüşüm matrislerini oluşturup daha sonra tüm T1, T2, T3, ...,Tn dönüşüm matrislerinin çarpılmasıyla ardışık dönüşüm matrisini elde ediyoruz. Sonuç olarak bulduğumuz matrisin 1. şekildeki gibi bir hal aldığını göreceksiniz. Burada matrisin T(1,4) = Px, T(2,4) = Py, T(3,4) = Pz robotun uç konum bilgilerini vermektedir.
Yapılmış bir örnek için youtube linkine tıklayabilirsiniz.
https://www.youtube.com/watch?v=Me5yjDgQFdQ
*notlar ( fotoğraftaki ) bana aittir.